Examples¶
You can find the examples detailed on this page and more in the
examples/ directory of SCOOP.
Please check the API Reference for any implentation detail of the proposed functions.
Introduction to the map() function¶
A core concept of task-based parallelism as presented in SCOOP is the
map. An introductory example to map working is presented in examples/map_doc.py.
1 2 3 4 5 6 7 8 9 | from __future__ import print_function
from scoop import futures
def helloWorld(value):
return "Hello World from Future #{0}".format(value)
if __name__ == "__main__":
returnValues = list(futures.map(helloWorld, range(16)))
print("\n".join(returnValues))
|
Line 1 allows Python 2 users to have a print function compatible with Python 3.
On line 2, SCOOP is imported.
On line 4-5, the function that will be mapped is declared.
The condition on line 7 is a safety barrier that prevents the main program to be executed on every workers. It ensures that the map is issued only by one worker, the root.
The map() function is located on line 8.
It launches the helloWorld function 16 times, each time with a different
argument value selected from the range(16) argument.
This method is compatible with the standard Python map() function and thus
can be seamlessly interchanged without modifying its arguments.
The example then prints the return values of every calls on line 9.
You can launch this program using python -m scoop. The output should look like this:
~/scoop/examples$ python -m scoop -n 8 map_doc.py
Hello World from Future #0
Hello World from Future #1
Hello World from Future #2
[...]
Note
Results of a map are always ordered even if their computation was made asynchronously on multiple computers.
Note
You can toy around with the previous example by changing the second parameter
of the map() function. Is it working with string arrays,
pure strings or other variable types?
Computation of 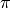 ¶
¶
A Monte-Carlo method to
calculate 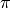 using SCOOP to parallelize its computation is found in
using SCOOP to parallelize its computation is found in
examples/pi_calc.py.
You should familiarize yourself with
Monte-Carlo methods before
going forth with this example.
First, we need to import the needed functions as such:
1 2 3 | from math import hypot
from random import random
from scoop import futures
|
The Monte-Carlo method is
then defined. It spawns two pseudo-random numbers that are fed to the
hypot function which
calculates the hypotenuse of its parameters.
This step computes the
Pythagorean equation
(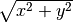 ) of the given parameters to find the distance from the
origin (0,0) to the randomly placed point (which X and Y values were generated
from the two pseudo-random values).
Then, the result is compared to one to evaluate if this point is inside or
outside the unit disk.
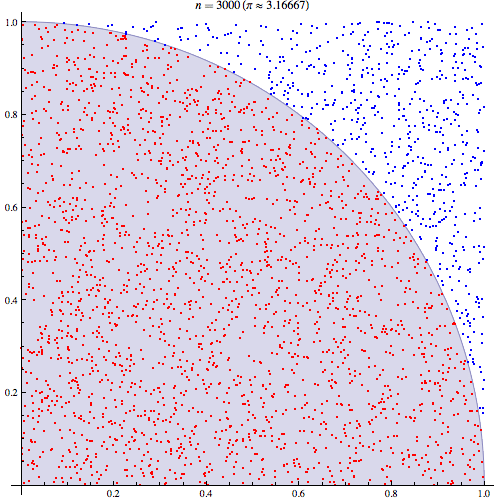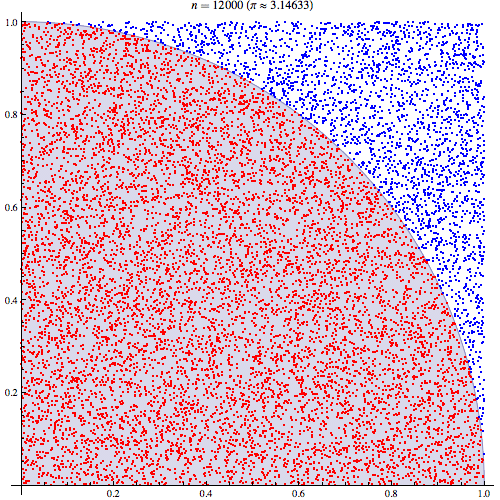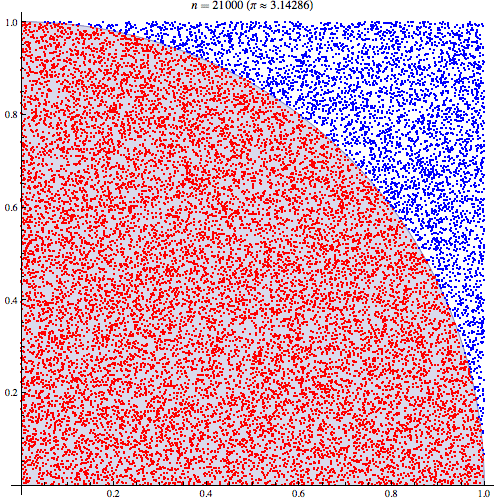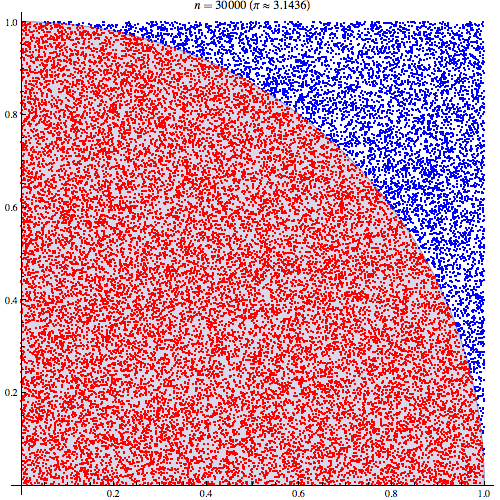
If it is inside (have a distance from the origin lesser than one), a value of
one is produced (red dots in the figure), otherwise the value is zero (blue dots
in the figure).
The experiment is repeated
) of the given parameters to find the distance from the
origin (0,0) to the randomly placed point (which X and Y values were generated
from the two pseudo-random values).
Then, the result is compared to one to evaluate if this point is inside or
outside the unit disk.
If it is inside (have a distance from the origin lesser than one), a value of
one is produced (red dots in the figure), otherwise the value is zero (blue dots
in the figure).
The experiment is repeated tries number of times with new random values.
The function returns the number times a pseudo-randomly generated point fell inside the unit disk for a given number of tries.
1 2 | def test(tries):
return sum(hypot(random(), random()) < 1 for _ in range(tries))
|
One way to obtain a more precise result with a
Monte-Carlo method is to
perform the method multiple times. The following function executes repeatedly
the previous function to gain more precision.
These calls are handled by SCOOP using it’s map()
function.
The results, that is the number of times a random distribution over a 1x1
square hits the unit disk over a
given number of tries, are then summed and divided by the total of tries.
Since we only covered the upper right quadrant of the
unit disk because both parameters
are positive in a cartesian map, the result must be multiplied by 4 to get the
relation between area and circumference, namely
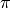 .
.
1 2 3 | def calcPi(nbFutures, tries):
expr = futures.map(test, [tries] * nbFutures)
return 4. * sum(expr) / float(nbFutures * tries)
|
As previously stated, you must wrap your code with a test for the __main__ name.
1 2 | if __name__ == "__main__":
print("pi = {}".format(calcPi(3000, 5000)))
|
You can now run your code using the command python -m scoop.
Sharing Constant¶
A typical usage of the shared constants is to broadcast a value or an object that must be created at runtime and read by every worker, as the following:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
def getValue(words):
"""Computes the sum of the values of the words."""
value = 0
for word in words:
for letter in word:
# shared.getConst will evaluate to the dictionary broadcasted by
# the root Future
value += shared.getConst('lettersValue')[letter]
return value
if __name__ == "__main__":
# Set the values of the letters according to the language and broadcast it
# This list is set at runtime
import sys
if len(sys.argv) > 1 and sys.argv[1] == 'francais':
shared.setConst(lettersValue={'a': 1, 'b': 3, 'c': 3, 'd': 2, 'e': 1,
'f': 4, 'g': 2, 'h': 4, 'i': 1, 'j': 8, 'k':10, 'l': 1, 'm': 2, 'n': 1,
'o': 1, 'p': 3, 'q': 8, 'r': 1, 'r': 1, 's': 1, 't': 1, 'u': 1, 'v': 4,
'w':10, 'x':10, 'y':10, 'z': 10})
print("French letter values used.")
else:
shared.setConst(lettersValue={'a': 1, 'b': 3, 'c': 3, 'd': 2, 'e': 1,
'f': 4, 'g': 2, 'h': 4, 'i': 1, 'j': 8, 'k': 5, 'l': 1, 'm': 3, 'n': 1,
'o': 1, 'p': 3, 'q':10, 'r': 1, 'r': 1, 's': 1, 't': 1, 'u': 1, 'v': 4,
'w': 4, 'x': 8, 'y': 4, 'z': 10})
print("English letter values used.")
# Get the player words (generate a list of random letters
import random
import string
random.seed(3141592653)
words = []
player_quantity = 4
words_per_player = 10
word_letters = (1, 6)
for pid in range(player_quantity):
player = []
for _ in range(words_per_player):
word = "".join(random.choice(string.ascii_lowercase) for _ in range(random.randint(*word_letters)))
player.append(word)
print("Player {pid} played words: {player}".format(**locals()))
words.append(player)
# Compute the score of every player and display it
results = list(futures.map(getValue, words))
for pid, result in enumerate(results):
print("Player {pid}: {result}".format(**locals()))
|
Overall example¶
The examples/fullTree.py example holds a wrap-up of available SCOOP functionnalities.
It notably shows that SCOOP is capable of handling twisted and complex
hierarchical requirements.
Getting acquainted with the previous examples is fairly enough to use SCOOP, no need to dive into this complicated example.
 Project Homepage
Project Homepage